More projects to be posted soon! (Last updated: April 2025)

A Framework for Evaluating Human Driver Models using Neuroimaging

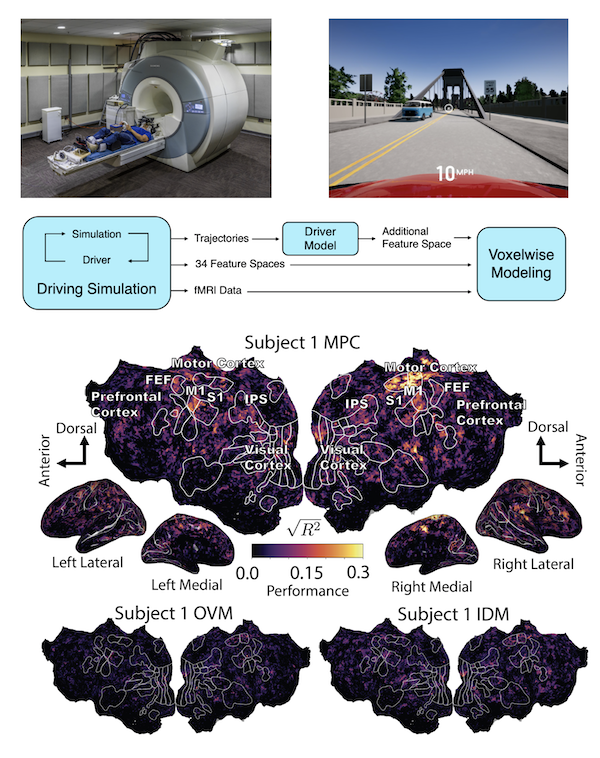Driving is a complex task which requires synthesizing multiple senses, safely reasoning about the behavior of others, and adapting to a constantly changing environment. Failures of human driving models can become failures of vehicle safety features or autonomous driving systems that rely on their predictions. Although there has been a variety of work to model human drivers, it can be challenging to determine to what extent they truly resemble the humans they attempt to mimic. The development of improved human driver models can serve as a step towards better vehicle safety. In order to better compare and develop driver models, we propose going beyond driving behavior to examine how well these models reflect the cognitive activity of human drivers. In particular, we compare features extracted from human driver models with brain activity as measured by functional magnetic resonance imaging. We have explored this approach on three traditional control-theoretic human driver models as well as on an end to end modular deep learning based driver model. We hope to explore both how human driver models can inform our understanding of brain activity and how better understanding brain activity can help us design better human driver models.

Point of contact: Christopher Strong, Kaylene Stocking

Read more here.

Certifiable Learning for High-Dimensional Reachability Analysis

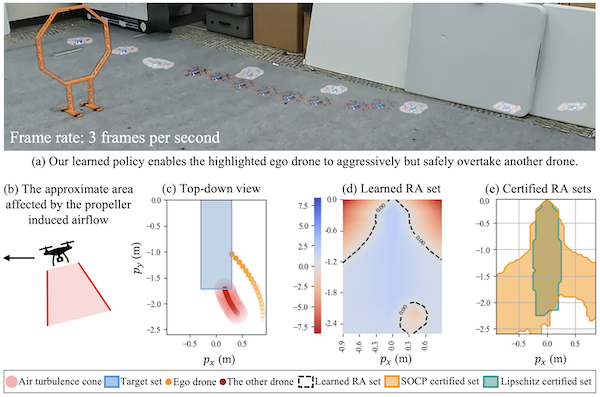Ensuring the safe operation of robotic systems in uncertain environments is critical for human-centered autonomy—whether it’s humanoid robots working closely with people or air taxis navigating crowded skies. Classical Hamilton-Jacobi reachability analysis provides rigorous safety verification, but its curse of dimensionality makes it impractical for high-dimensional systems. To overcome this, we leverage scalable deep reinforcement learning techniques to learn our newly designed reachability value function, featuring properties such as Lipschitz continuity and fast-reaching guarantees. Recognizing the black-box nature of most deep learning methods, we enhance the credibility of our learned reachability sets by designing computationally efficient post-learning certification methods. These real-time computable certification techniques deliver deterministic safety guarantees under worst-case disturbances. Looking ahead, our two-stage process (i.e., reachability learning followed by post-learning certification) sheds light on designing next-generation reachability analysis tools that scale to complex, uncertain, and high-dimensional safety-critical autonomous systems, with strong verifiable assurance.

Point of contact: Jingqi Li

Read more here.

Hacking Predictors Mean Hacking Cars

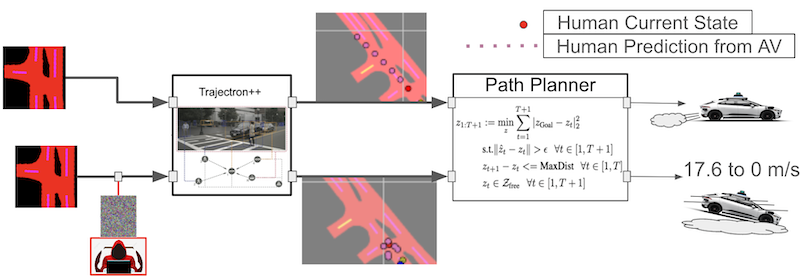Adversarial attacks on learning-based multi-modal trajectory predictors have already been demonstrated. However, there are still open questions about the effects of perturbations on inputs other than state histories, and how these attacks impact downstream planning and control. In this paper, we conduct a sensitivity analysis on two trajectory prediction models, Trajectron++ and AgentFormer. The analysis reveals that between all inputs, almost all of the perturbation sensitivities for both models lie only within the most recent position and velocity states. We additionally demonstrate that, despite dominant sensitivity on state history perturbations, an undetectable image map perturbation made with the Fast Gradient Sign Method can induce large prediction error increases in both models, revealing that these trajectory predictors are, in fact, susceptible to image-based attacks. Using an optimization-based planner and example perturbations crafted from sensitivity results, we show how these attacks can cause a vehicle to come to a sudden stop from moderate driving speeds.

Point of contact: Marsalis Gibson

Competency-Aware Planning for Probabilistically Safe Navigation Under Perception Uncertainty

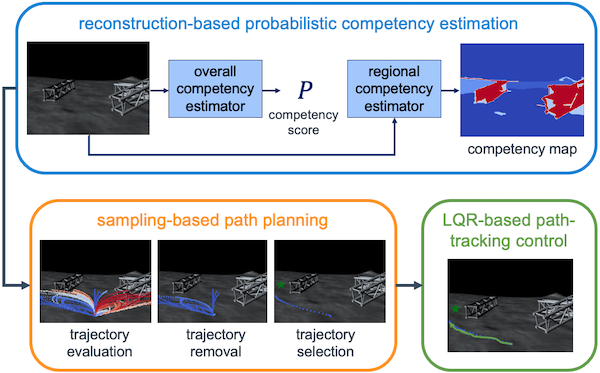Perception-based navigation systems are useful for unmanned ground vehicle (UGV) navigation in complex terrains, where traditional depth-based navigation schemes are insufficient. However, these data-driven methods are highly dependent on their training data and can fail in surprising and dramatic ways with little warning. To ensure the safety of the vehicle and the surrounding environment, it is imperative that the navigation system is able to recognize the predictive uncertainty of the perception model and respond safely and effectively in the face of uncertainty. In an effort to enable safe navigation under perception uncertainty, we develop a probabilistic and reconstruction-based competency estimation (PaRCE) method to estimate the model’s level of familiarity with an input image as a whole and with specific regions in the image. We find that the overall competency score can accurately predict correctly classified, misclassified, and out-of-distribution (OOD) samples. We also confirm that the regional competency maps can accurately distinguish between familiar and unfamiliar regions across images. We then use this competency information to develop a planning and control scheme that enables effective navigation while maintaining a low probability of error. We find that the competency-aware scheme greatly reduces the number of collisions with unfamiliar obstacles, compared to a baseline controller with no competency awareness. Furthermore, the regional competency information is particularly valuable in enabling efficient navigation.

Point of contact: Sara Pohland

Read more here.

System-Level Analysis of Module Uncertainty Quantification in the Autonomy Pipeline

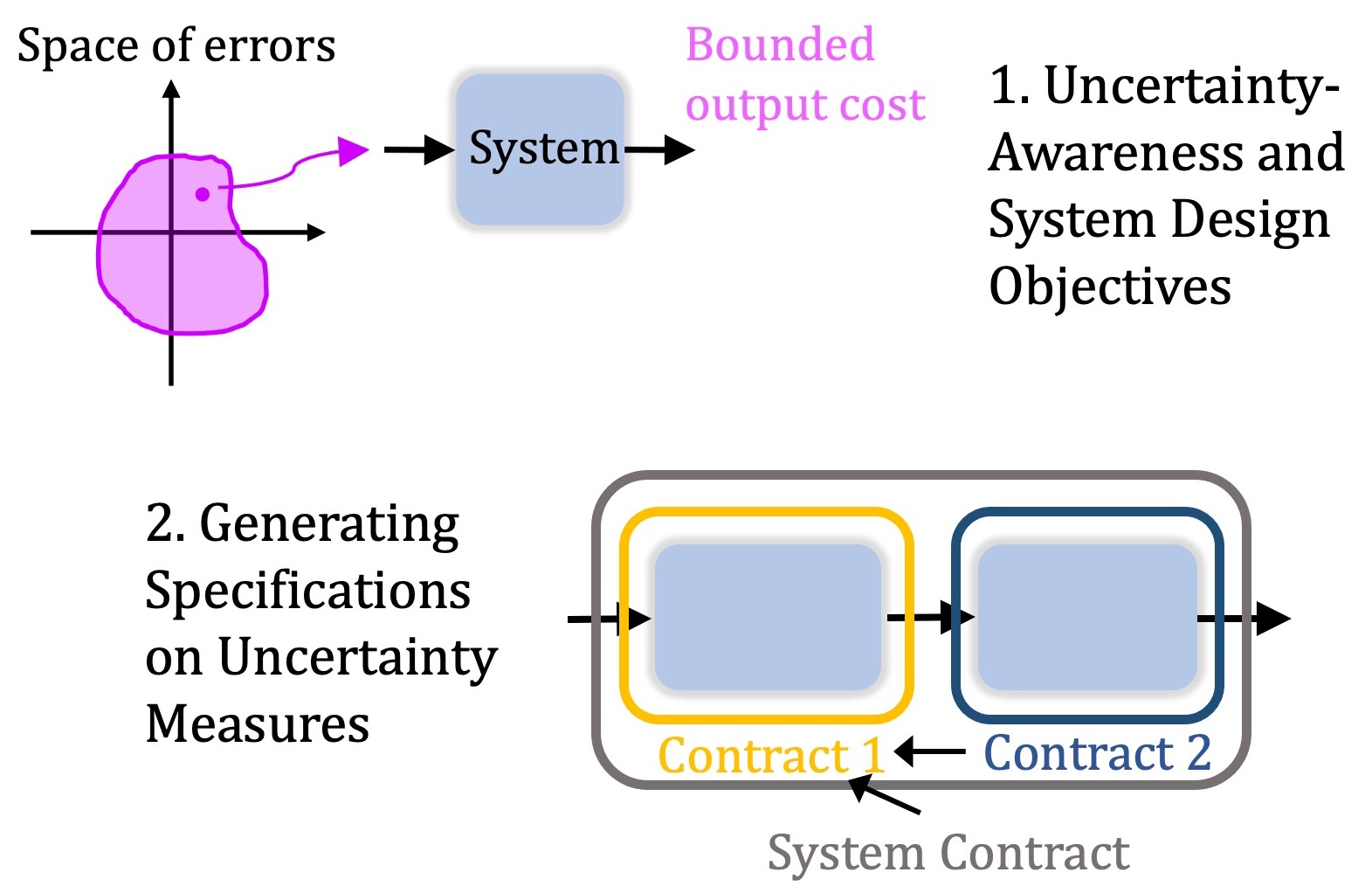Many autonomous systems are designed as modularized pipelines with learned components. In order to assure the safe operation of these systems, a common approach is to perform uncertainty quantification for the learned modules and then use the uncertainty measures in the downstream modules. However, uncertainty quantification is not well understood and the produced uncertainty measures can often be unintuitive. In this work, we contextualize uncertainty measures by viewing them from the perspective of the overall system design and operation. We propose two analysis techniques to do so. In our first analysis, we connect uncertainty quantification with system design objectives by proposing a measure of system robustness and then using this metric to compare different system designs. Using an autonomous driving system as our testbed, we use the new metric to show how being uncertainty-aware can make a system more robust. In our second analysis, we generate a specification on the uncertainty measure for a specific module given a system specification. We analyze another real-world and complex system, a system for aircraft runway incursion detection. We show how our formalism allows a designer to simultaneously constrain the properties of the uncertainty measure and analyze the efficacy of the decision-making-under-uncertainty algorithm used by the system.

Point of contact: Sampada Deglurkar

Read more here.

Modeling and Control System Design of Modern Power Systems

Many autonomous Modern power systems can be characterized by their accelerated incorporation of renewable energy resources at the generation level, and electronics such as data centers and EVs at the load level. This represents a large shift in the way they behave, and how they need to be operated. Therefore, new engineering requirements are needed so that we can reliably operate the power grid in the face of change. Some of these needs include the modeling of new devices, their control, and studying how they fit into the existing grid. In our lab, we work on modeling power system components so that we can execute control, and perform stability analyses in order to provide recommendations as to how to operate the grid moving forward. Examples of our work include hybrid control of inverters, and high-fidelity modeling of transmission lines and loads.

Point of contact: Gabriel Enrique Colon-Reyes

Load Model-Independent Power System Regions of Attraction

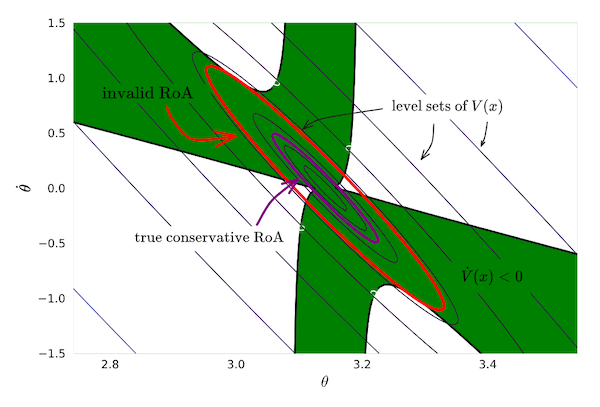Power system load modeling is difficult because it is impossible to know the details of all loads, let alone model them from first principles. As a result, many approximate lumped load models have been developed to attempt to capture the true behavior of the grid. These models have similar forms worldwide, but there is no industry standard for which parameters are most accurate. As the particular choice of parameters has a significant impact on the validity of simulation results, particularly in transient simulations, we seek to find a set in state space which is within the region of attraction of the operating point for a variety of different load model parameters. Currently, we consider the ZIP family of load models, and hope to find a region of attraction that functions for all linear combinations of Z (constant impedance), I (constant current) and P (constant power) loads. We develop an optimization-based method using quadratic Lyapunov functions to compute this conservative region of attraction for the general case of ODE systems on the order of 25 states.

Point of contact: Reid Dye

Control Barrier-Value Function: Unified Safety Certificate Function

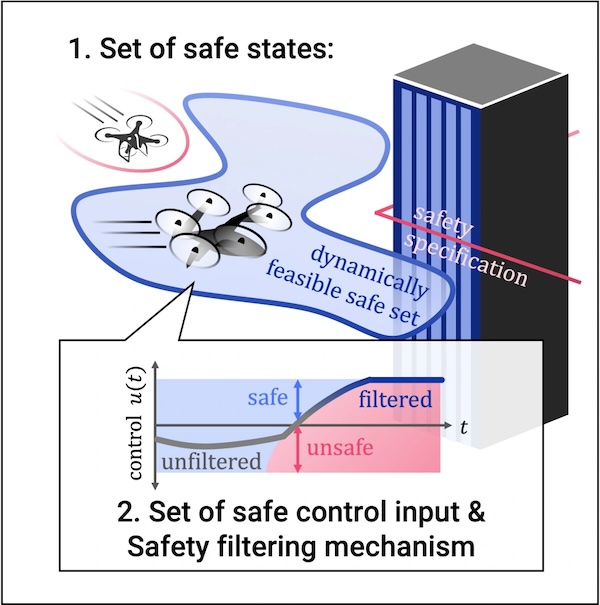At the core of dynamical system safety assurance is verifying a 1) dynamically feasible safe set where the system can indefinitely remain, and 2) designing a controller (or constraint on the control input) to realize it. Many model-based approaches use the concept of a certificate function, a scalar function whose level sets characterize the safe domain, and whose gradient can impose a constraint on the control input to ensure safety. Control Barrier Functions (CBFs) and Hamilton-Jacobi (HJ) reachability value functions are two prominent choices of the certificate functions. CBFs’ key concept is to constrain the robot to "smoothly brake" before it exits the safe domain. While this mechanism is easy to implement, constructing a valid CBF is challenging. In contrast, HJ reachability constructs a maximal safe set that meets safety specifications. However, the optimal control derived from its value function is often too conservative for practical use. A line of our research aims at bridging the gap between CBFs and HJ reachability, using the best of both methods. We discovered that the CBF braking mechanism can be incorporated into the reachability formulation, which makes it feasible to use its (set-valued) optimal policy as the safety filter. Moreover, we discovered that all CBFs can be interpreted as reachability value functions. An important accompanying finding is that in this interpretation, discount factors in reachability play a crucial role, and they can help design machine learning-based approximate DP algorithms like to have good convergence properties.

Point of contact: Jason J. Choi

Read more here.

Efficient Iterative Linear-Quadratic Approximations for Nonlinear Multi-Player General-Sum Differential Games

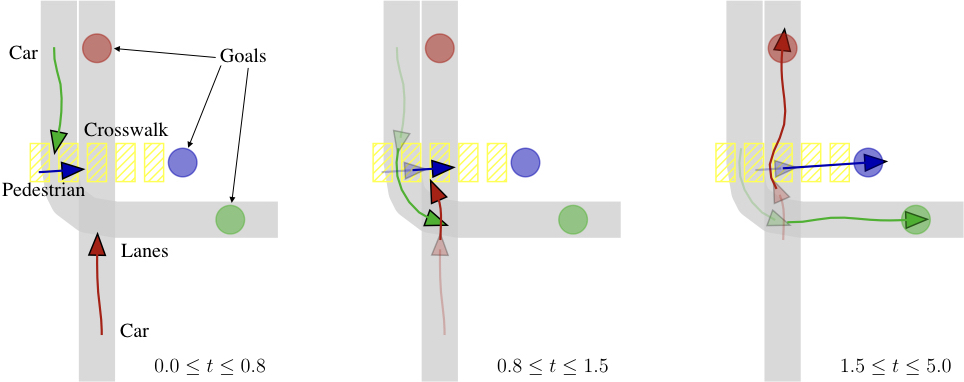Many problems in robotics involve multiple decision making agents. To operate efficiently in such settings, robots must reason about the impact of their decisions on the behavior of other agents. Differential games offer an expressive theoretical framework for formulating these types of multi-agent problems. Unfortunately, most numerical solution techniques scale poorly with state dimension and are rarely used in real-time applications. For this reason, it is common to predict the future decisions of other agents and solve the resulting decoupled, i.e., single-agent, optimal control problem. This decoupling neglects the underlying interactive nature of the problem; however, efficient solution techniques do exist for broad classes of optimal control problems. We take inspiration from one such technique, the iterative linear-quadratic regulator (ILQR), which solves repeated approxima-tions with linear dynamics and quadratic costs. Similarly, our proposed algorithm solves repeated linear-quadratic games. We experimentally benchmark our algorithm in several examples with a variety of initial conditions and show that the resulting strategies exhibit complex interactive behavior. Our results indicate that our algorithm converges reliably and runs in real-time. In a three-player, 14-state simulated intersection problem, our algorithm initially converges in < 0.75 s. Receding horizon invocations converge in < 50 ms in a hardware collision-avoidance test.

Read more here.

Risk-Sensitive Safety Analysis

An important problem is to quantify how safe a dynamic system can be despite real-world uncertainties and to synthesize control policies that ensure safe operation. Existing approaches typically assume either a worst-case perspective (which can yield conservative solutions) or a risk-neutral perspective (which neglects rare events). An improved approach would seek a middle ground that allows practitioners to modify the assumed level of conservativeness as needed. To this end, we have developed a new risk-sensitive approach to safety analysis that facilitates a tunable balance between the worst-case and risk-neutral perspectives by leveraging the Conditional Value-at-Risk (CVaR) measure. This work proposes risk-sensitive safety specifications for stochastic systems that penalize one-sided tail risk of the cost incurred by the system’s state trajectory. The theoretical contributions have been to prove that the safety specifications can be under-approximated by the solution to a CVaR-Markov decision process, and to prove that a value iteration algorithm solves the reduced problem and enables tractable risk-sensitive policy synthesis for a class of linear systems. A key empirical contribution has been to show that the approach can be applied to non-linear systems by developing a realistic numerical example of an urban water system. The water system and a thermostatically controlled load system have been used to compare the CVaR criterion to the standard risk-sensitive criterion that penalizes mean-variance (exponential disutility). Numerical experiments demonstrate that reducing the mean and variance is not guaranteed to minimize the mean of the more harmful cost realizations. Fortunately, however, the CVaR criterion ensures that this safety-critical tail risk will be minimized, if the cost distribution is continuous.

Read more here.

FaSTrack: a Modular Framework for Fast and Guaranteed Safe Motion Planning

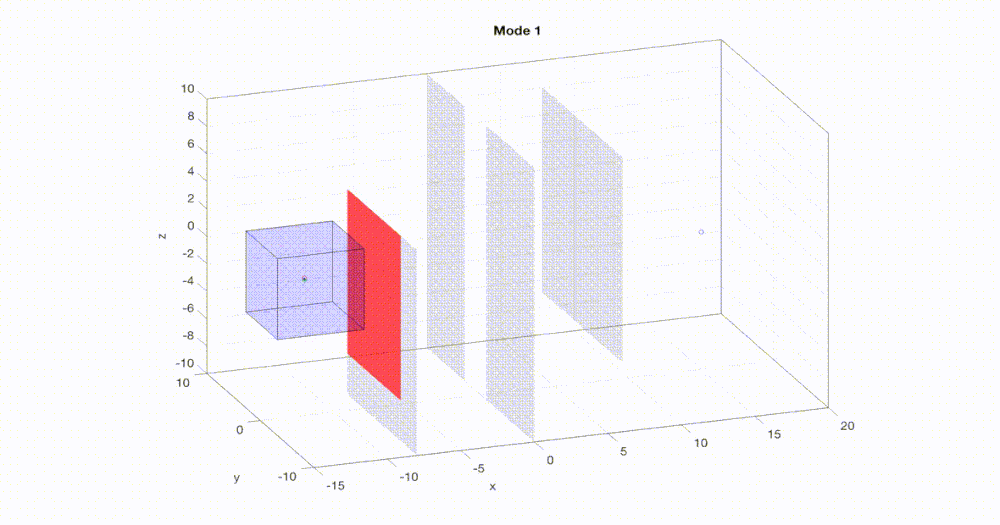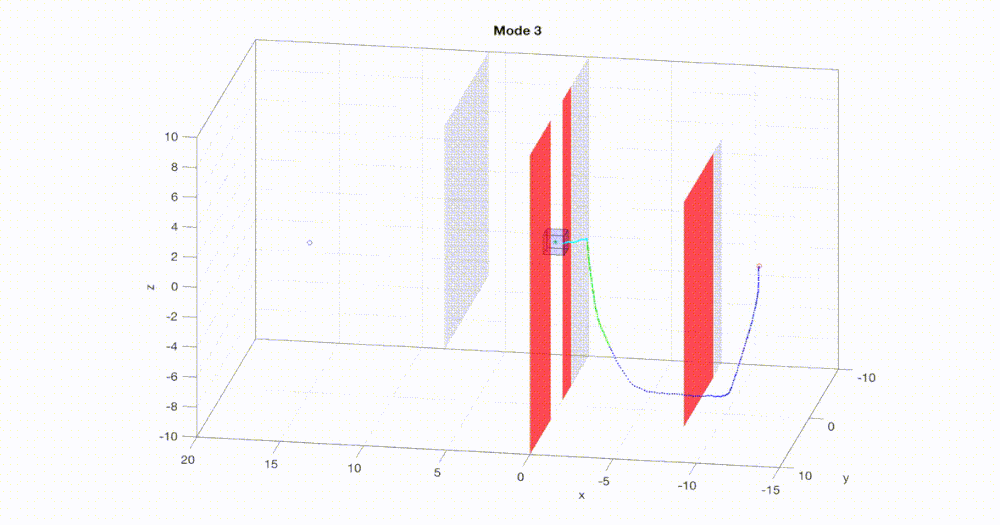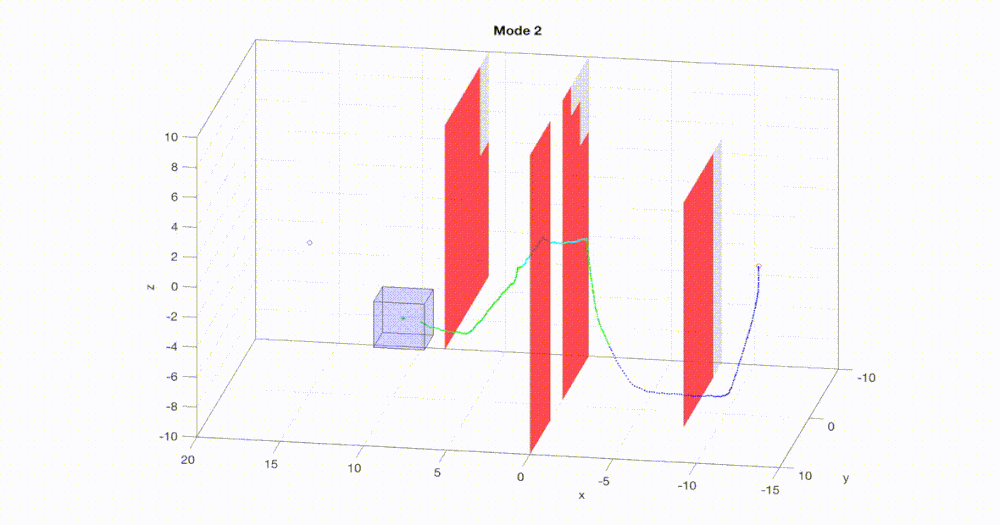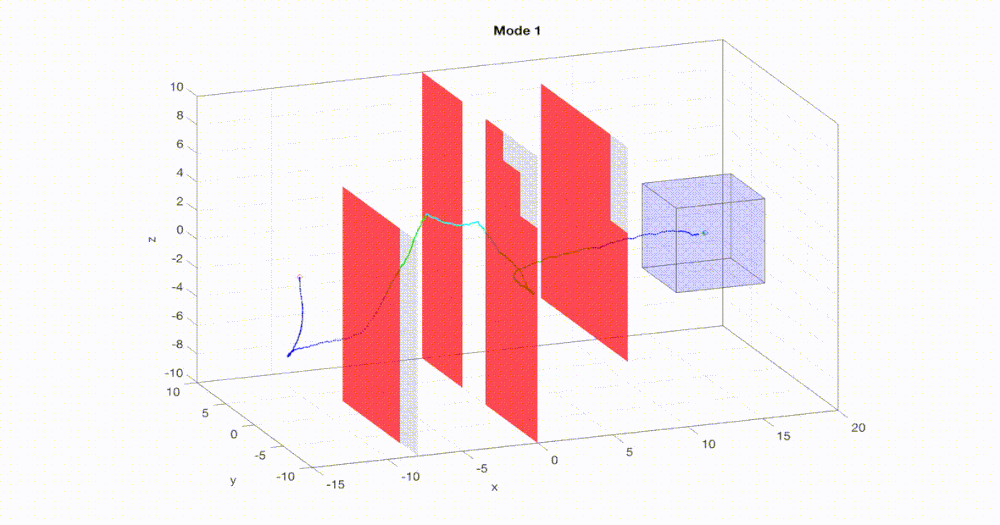Fast and safe navigation of dynamical systems through a priori unknown cluttered environments is vital to many applications of autonomous systems. However, trajectory planning for autonomous systems is computationally intensive, often requiring simplified dynamics that sacrifice safety and dynamic feasibility in order to plan efficiently. Conversely, safe trajectories can be computed using more sophisticated dynamic models, but this is typically too slow to be used for real-time planning. We propose a new algorithm FaSTrack: Fast and Safe Tracking for High Dimensional systems. A path or trajectory planner using simplified dynamics to plan quickly can be incorporated into the FaSTrack framework, which provides a safety controller for the vehicle along with a guaranteed tracking error bound. This bound captures all possible deviations due to high dimensional dynamics and external disturbances. Note that FaSTrack is modular and can be used with most current path or trajectory planners. We demonstrate this framework using a 10D nonlinear quadrotor model tracking a 3D path obtained from an RRT planner.

Read more here.

Probabilistically Safe Robot Planning with Confidence Based Human Predictions

In order to safely operate around humans, robots can employ predictive models of human motion. Unfortunately, these models cannot capture the full complexity of human behavior and necessarily introduce simplifying assumptions. As a result, predictions may degrade whenever the observed human behavior departs from the assumed structure, which can have negative implications for safety. In this paper, we observe that how "rational" human actions appear under a particular model can be viewed as an indicator of that model's ability to describe the human's current motion. By reasoning about this model confidence in a real-time Bayesian framework, we show that the robot can very quickly modulate its predictions to become more uncertain when the model performs poorly. Building on recent work in provably-safe trajectory planning, we leverage these confidence-aware human motion predictions to generate assured autonomous robot motion. Our new analysis combines worst-case tracking error guarantees for the physical robot with probabilistic time-varying human predictions, yielding a quantitative, probabilistic safety certificate. We demonstrate our approach with a quadcopter navigating around a human.

Read more here.